
1. 시간복잡도란? (Time complexity)
알고리즘 문제를 풀 때 예상 입출력 케이스를 코드 실행을 통해 통과 했음을 확인했어도 정작 코드 제출을 하면 효율성에서 시간초과로 통과하지 못하는 경우가 있다.
우리가 작성한 코드는 실행시간이 얼마나 걸릴까?
입력값과 연산 수행 시간의 상관관계를 나타내는 척도를 시간 복잡도라고 한다.
2. 시간복잡도 표현방법
점근적 표기법(3가지)로 시간복잡도를 나타내는데 사용된다.
- 최상의 경우 : 오메가 표기법 (Big-Ω Notation)
- 평균의 경우 : 세타 표기법 (Big-θ Notation)
- 최악의 경우 : 빅오 표기법 (Big-O Notation)
평균인 세타 표기법을 사용한다고 생각할 수 도 있는데 평가하기 까다롭다는 판단이다.
평균은 최상과 최악의 평균값으로 시간복잡도는 최악을 기준으로 "빅오 표기법" 으로 판단하여 성능을 예측한다.
3. 빅오 표기법(Big-O)
빅오 표기법은 불필요한 연산을 제거하여 알고리즘 분석을 쉽게 할 목적으로 사용된다.
Big-O로 측정되는 복잡성에는 시간과 공간복잡도가 있는데 ,
시간복잡도는 입력된 N의 크기에 따라 실행되는 조작의 수를 나타낸다.
공간복잡도는 알고리즘이 실행될 때 사용하는 메모리의 양을 나타낸다.
요즘에는 데이터를 저장할 수 있는 메모리의 발전으로 중요도가 낮아졌다.
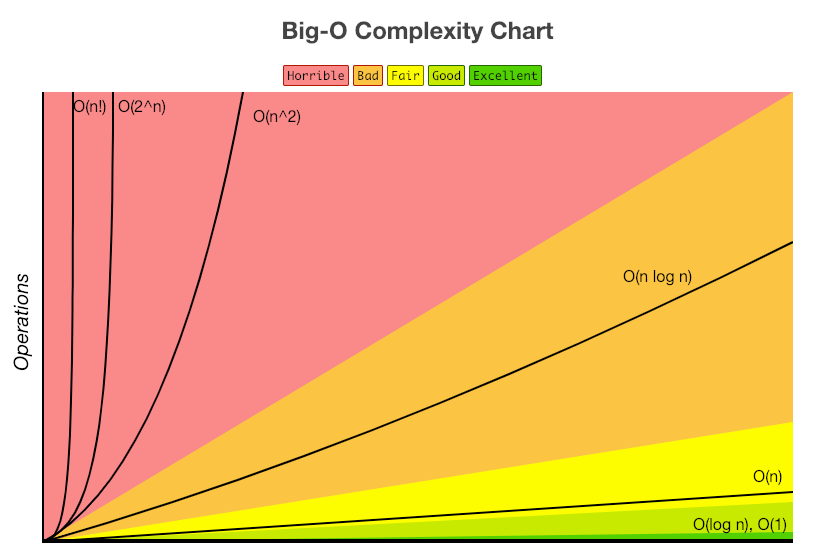
알고리즘을 수행하기 위해 프로세스가 수행해야 하는 연산을 수치화 한것이다.
실행시간이 아닌 연산횟수 수치로 판별하는 이유는?
실행시간은 컴퓨터의 하드웨어 또는 프로그래밍 언어에 따라 편차가 달라지기 때문에 명령어의 연산 횟수를 나타낸다.
시간복잡도 단계 (빠른순으로)
[fast] O(1) < O( log n ) < O(n) < O(n log n) < O(n^2)
O(1) – 상수 시간 : 문제를 해결하는데 오직 한 단계만 처리함.
O(log n) – 로그 시간 : 문제를 해결하는데 필요한 단계들이 연산마다 특정 요인에 의해 줄어듬.
O(n) – 직선적 시간 : 문제를 해결하기 위한 단계의 수와 입력값 n이 1:1 관계를 가짐.
O(n log n) - 선형로그형: 문제를 해결하기 위한 단계의 수가 N*(log2N) 번만큼의 수행시간을 가진다.
O(n^2) – 2차 시간 : 문제를 해결하기 위한 단계의 수는 입력값 n의 제곱.
3-1. O(1) 상수시간 예제코드 및 계산법
const sum = (N+1) * N / 2;(N+1)이 1번, * N 이 1번, /2가 1번, = 가 1번
합쳐서 총 4번의 연산이 수행된다. Big-O 표기법으로 표현하면 4 = O(1)이다.
3-2. O(log n) 로그시간 예제코드 및 계산법(실행시간이 입력크기의 로그에 비례 )
알고리즘의 각 단계에서 입력의 상당부분(절반)을 방문하지 않고 지나간다. (예: 이진탐색 알고리즘)
O(log n)은 밑이 2인 log2 n 을 일반적으로 나타낸다.
그러나, Big-O 표기법에서 로그의 밑은 그다지 중요하지 않다. 즉, 점근 표기법에서 log의 밑은 의미에 크게 영향을 주지 않으므로 신경쓰지 않아도 된다.
function fucName(n) {
let i = 1; // 1
while(i < n) { // log2 n
console.log(i); // log2 n
i = i * 2; // log2 n
}
}i = i * 2로 인해 숫자는 1 -> 2 -> 4 -> 8...인 2의 거듭제곱으로 커지기 때문에 while문은 log2(로그 밑)n 만큼 반복된다.
1 + (log2 n ) + log2 n + log2 n = 3log2 n + 1 => (빅오표기법 상수는 다 무시하므로) O(log n)
3-3. O(n) 로그시간 예제코드 및 계산법
let sum = 0;
for(let i = 0; i <= N; i++) {
sum += i;
}sum=0 1번, let i = 0 1번, i++ N번, sum += i가 N번
총 2N+2번의 연산이 수행되므로 상수 무시하고 O(N) 이다.
3-4. O(nlogn) 선형 로그시간 예제 및 계산법(실행시간이 입력크가와 입력크기의 로그 곱에 비례)
입력의 절반(또는 일부)으로 나눌때마다 각 부분을 독립적으로 처리(예: 병합정렬, 퀵정렬, 힙정렬)
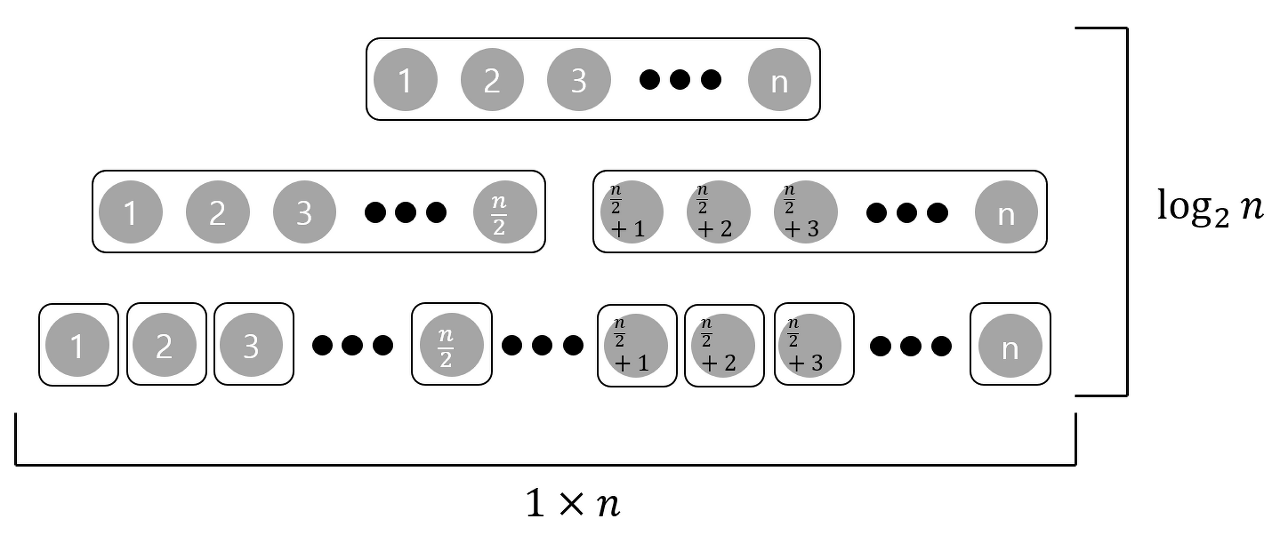
합병 정렬은 더이상 나눌 수 없을때까지 두개의 부분 리스트로 나누다가 더이상 나눌 수 없게 되면 다시 나눈 순서대로 합치는 정렬이다.
합치는 방법은 두개의 부분 리스트의 제일 앞 원소를 비교하며 더 작은 원소를 새로운 리스트에 포함시키는 것!
// 아래와 같은 리스트가 있다고 가정할 때,
const arr = [1 9 5 3 2 4 7 6];
// 1번: 1 9 5 3 | 2 4 7 6
// 2번: 1 9 | 5 3 | 2 4 | 7 6
// 3번: 1 | 9 | 5 | 3 | 2 | 4 | 7 | 6 각각의 부분리스트의 원소갯수가 1이 되었으니 더이상 나눌 수 없습니다.
여기서 전부 1개의 부분집합으로 만드는데 필요한 연산의 개수는 밑이 2인 log n 입니다. 편의상 log_2 n 이라 하겠습니다.
※ 만약 왜 log_2 n인지 이해가 가지 않으실 때만 읽어보세요!
병합정렬이 나누는데 필요한 연산 횟수는 'n개의 원소를 가진 리스트'를 계속 반으로 나눠 '1개의 원소를 가진 리스트'들로 만드는 데 필요한 횟수입니다.
그래도 이해가 가지 않으신다면 로그에 대한 개념이 약하신 것이라고 생각합니다.
log_2 n는 2를 밑, n을 어떤수라고 하면 "2(밑)을 몇번 곱해야 n(어떤수)를 만들 수 있습니까?" 라는 말로 풀어쓸 수 있습니다.
말을 살짝 뒤집어보면 " n(어떤수)를 2(밑)으로 몇번 나눠야 1을 만들 수 있습니까?" 가 되는데요.
연산횟수를 구하는 방법인 n개의 원소를 반으로 계속 나눠서 1개의 원소로 나누는데 필요한 횟수 와 똑같은 말입니다.출처: https://www.codeit.kr/community/questions/UXVlc3Rpb246NWUzNDUyMjU4MGU1MTMzNzNkOTYyZTcz
3-5. O(n^2) 이차 시간 예제코드 및 계산법
알고리즘의 실행시간이 입력 크기의 제곱에 비례 , 각 원소를 다른 모든 원소와 비교하는 경우 (예: 버블 정렬, 선택정렬, 삽입정렬)
function fucName(n) {
for(let i = 0; i < n.length; i++) {
for(let j = 0; j < n.length; j++ {
console.log(i,j);
}
}
}위와 같이 반복문이 두 번 있는 케이스(각 원소를 다른 모든 원소와 비교하는 경우)는 시간복잡도가 O(n^2)이다.
잘못된 정보에 대한 피드백은 언제나 환영입니다 (´▽`ʃƪ)♡
참고 게시글:
https://blog.chulgil.me/algorithm/,
https://todaycode.tistory.com/45,
'내직업은 IT종사자 > 알고리즘.자료구조' 카테고리의 다른 글
| [algorithm] stack(스택)이란? 사용 예제/방법 (javascript 코드) (0) | 2023.04.11 |
|---|---|
| [algorithm] 해시테이블 자료구조 란? (0) | 2023.03.10 |
| [알고리즘 코딩테스트 꿀팁] 코딩테스트 잘보는 법 TIP (2) | 2023.03.06 |


